Función de verosimilitud y log-verosimilitud
Distribución Poisson y Geométrica
Estimación de Máxima Verosimilitud (MLE)
Definición 1. Según Kleinbaum y Klein (2010, 128) “the method of maximum likelihood chooses that estimator of the set of unknown parameters \(\theta\) which maximizes the likelihood function \(\mathcal{L}(\theta)\). The estimator is denoted as \(\hat{\theta}\).” De esta forma, la función de máxima verosimilitud se puede expresar tal que
\[ \mathcal{L}(\theta)=P(X_1=x_1,\ldots,X_n=x_n)=f(x_1;\theta)\cdot \ldots \cdot f(x_n;\theta)=\prod\limits_{i=1}^n f(x_i;\theta) \]
donde \(f(x_{i}; \theta)\) es la función de masa o densidad asociada a la variable aleatoria \(X\).
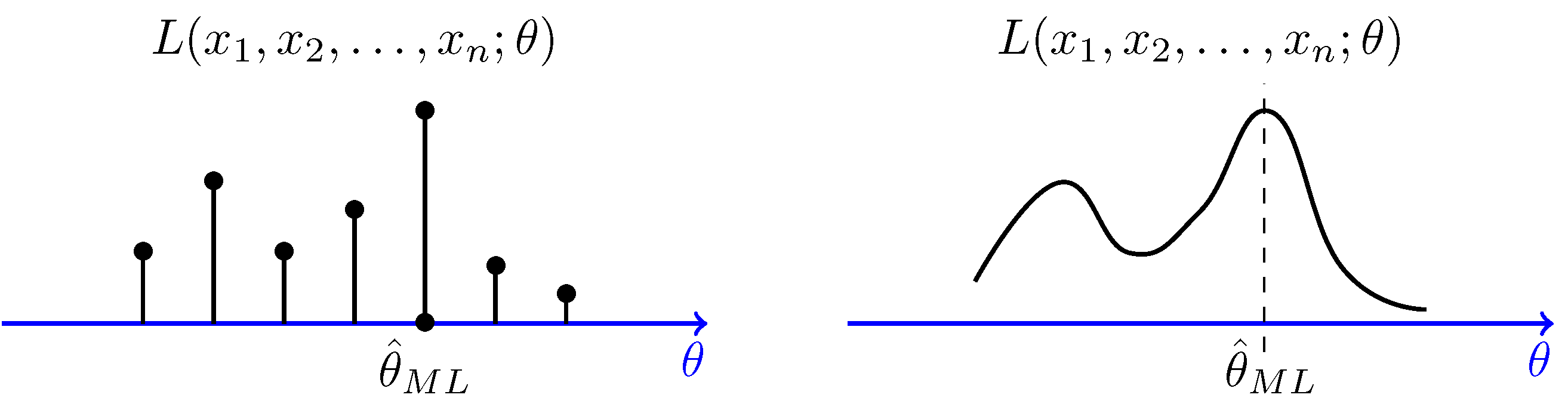
Asimismo, al valor que máxima la función de verosimilitud se le llama “estimador máximo verosímil”. Normalmente se denota con \(\hat{\theta}\) y matemáticamente se representa tal que
\[ \hat{\theta}:= \arg \max \mathcal{L}(\theta). \]
Distribución Poisson
Definición 2. Sea \(X\) una variable aleatoria discreta que se distribuye de forma Poisson con parámetro \(\lambda\). Su función de masa de probabilidad está dada por
\[ f_{X}(x) = P(X = x \mid \lambda) = \dfrac{\lambda^{x} e^{-\lambda}}{x!} \quad \text{si} \quad x \in \mathbb{N}_{0} \quad \text{y} \quad \lambda > 0 \]
Además, la esperanza matemática (media) y varianza toman el mismo valor de \(\lambda\).1 Esto quiere decir que
1 A esta propiedad se le llama equisdisperción.
\[ \mu_{X} = \sigma^{2}_{X} = \lambda \]
Función de verosimilitud
Demostración 1. Suponga que \(X = (X_{1}, X_{2}, \ldots, X_{n}) \sim \text{Poisson}(\theta)\) con \(\theta\) desconocido. Muestre que la función de verosimilitud es
\[ \mathcal{L}(\theta) = \dfrac{\theta^{\sum\limits_{j=1}^{n}x_{j}} \exp{(-n\theta)}}{\prod_{j=1}^{n} x_{j}!} \] Además, determine que la función de log-verosimilitud y el estimador máximo verosímil (EMV) están expresados por las siguientes fórmulas, respectivamente
\[ \mathcal{l}(\theta) = \sum\limits_{j=1}^{n} x_{j} \log{(\theta)} - n\theta - \sum\limits_{j=1}^{n} x_{j}! \]
\[ \hat{\theta} = \dfrac{1}{n}\sum\limits_{j=1}^{n} x_{j} \]
Solución 1. Primeramente \(X_{j} \sim \text{Poiss}(\theta)\). Entonce tenemos que la función de verosimilitud es:
\[ \mathcal{L}(\theta) = \prod_{j=1}^{n} \dfrac{\theta^{x_{j}} \exp{(-\theta)}}{x_{j}!} = \dfrac{ \prod_{j=1}^{n} \theta^{x_{j}} \exp{\left(\prod_{j=1}^{n} -\theta\right)} }{ \prod_{j=1}^{n} x_{j}! } = \dfrac{\theta^{\sum\limits_{j=1}^{n}x_{j}} \exp{(-n\theta)}}{\prod_{j=1}^{n} x_{j}!} \]
Ahora, aplicamos \(\ln{\mathcal{L}(\theta)}\) para calcular la \(\mathcal{l}(\theta)\)
\[ \mathcal{l}(\theta) = \ln{\left[ \dfrac{\theta^{\sum\limits_{j=1}^{n}x_{j}} \exp{(-n\theta)}}{\prod_{j=1}^{n} x_{j}!} \right]} = \sum\limits_{j=1}^{n} x_{j} \log{(\theta)} - n\theta - \sum\limits_{j=1}^{n} x_{j}! \]
Luego podemos derivar \(\mathcal{l}(\theta)\) para encontrar el EMV que acompaña a esta distribución
\[ \dfrac{\partial \mathcal{l}(\theta)}{\partial \theta} = \left[ \sum\limits_{j=1}^{n} x_{j} \log{(\theta)} - n\theta - \sum\limits_{j=1}^{n} x_{j}! \right]^{'} = -n + \dfrac{1}{\theta} \sum\limits_{j=1}^{n} x_{j} \]
Posteriormente, se sabe que el EMV corresponde a \(\hat{\theta}:= \arg \max \mathcal{L}(\theta)\). Esto significa que hay que igualar a \(0\) la derivada anterior
\[ \dfrac{\partial \mathcal{l}(\theta)}{\partial \theta} = 0 \]
\[ \Rightarrow -n + \dfrac{1}{\theta} \sum\limits_{j=1}^{n} x_{j} = 0 \Rightarrow \dfrac{1}{n} \sum\limits_{j=1}^{n} x_{j} = \theta \Rightarrow \dfrac{1}{n} \sum\limits_{j=1}^{n} x_{j} = \hat{\theta} \]
Luego de obtener el estimador \(\hat{\theta}\) es necesario calcular la segunda derivada de \(\mathcal{l}(\theta)\) para poder corroborar que este valor corresponde al argumento que maximiza la log-verosimilitud de la distribución Poisson. Entonces
\[ \dfrac{\partial^{2} \mathcal{l}(\theta) }{\partial \theta^{2}} = -\dfrac{1}{\bar{x}^{2}} \sum\limits_{i=1}^{n} = \dfrac{n\bar{x}}{\bar{x}^{2}} = -\dfrac{n}{\bar{x}} < 0 \]
Finalmente, se muestra que EMV \(\hat{\theta}\) es el valor que maximiza la función de log-verosimilitud. En otras palabras
\[ \therefore \ \ \hat{\theta} = \dfrac{1}{n} \sum\limits_{j=1}^{n} x_{j} \]
Este valor \(\hat{\theta}\) corresponde a la media muestra de una distribución Poisson con parámetro \(\theta\).
Distribución Geométrica
Definición 3. Sea \(X = (X_{1}, \ldots, X_{n}) \sim \text{Geométrica}(p)\). Su función de masa de probabilidad está delimitada por la fórmula
\[ f_{X}(x;p) = p(1-p)^{x-1} \quad x\in \mathbb{N} \quad 0\leq p \leq1 \]
Ejercicio 1. Con base a esto responda
- Determine la función de verosimilitud de \(X\).
- Muestre que el EMV corresponde a \(\hat{p} = \dfrac{1}{\bar{x}_{n}}\).
- Verifique que \(\hat{p}\) sí es al estimador que máximiza la log-verosimilitud de \(X\).2
2 Sugerencia. Aplique la segunda deriva a la \(\mathcal{l}(p)\).
Ejercicios extras
Ejercicio 1.1. Sea \(X_{1}, \ldots, X_{n}\) una muestra aleatoria idénticamente distribuida con una función de densidad de probabilidad descrita por
\[ f_{X}(x_{i};\sigma) = \dfrac{1}{2\sigma} \exp{\left(-\dfrac{|x_{i}|}{\sigma}\right)} \quad i \in \mathbb{Z}^{+} \]
entonces, determine cuál es el EMV \(\hat{\sigma}\) que toma esta distribución.
Ejercicio 1.2. Dado \(X_{1}, \ldots, X_{n}\) una muestra aleatoria idénticamente distribuida con \(\theta\) desconocido y una función de densidad de probabilidad tal que
\[ \begin{equation} f(x;\theta) = \begin{cases} \dfrac{3x^{2}}{\theta^{3}} & \text{si $0 \leq x \leq \theta$}\\ 0 & \text{en otros casos}. \end{cases} \end{equation} \]
Muestre que la función de log-verosimilitud \(\mathcal{l}(\theta)\) toma la siguiente expresión
\[ \mathcal{l}(\theta) = n\ln{(3)} + \ln{\left(\prod_{i=1}^{n} x^{2}_{i}\right)} - 3n \ln{(\theta)} \]
Bibliografía
Cómo citar
@online{daniel rodríguez cruz2023,
author = {Daniel Rodríguez Cruz, Iván},
title = {Función de verosimilitud y log-verosimilitud},
date = {2023-04-03},
url = {https://ivanrodc.quarto.pub/idcr_blog_stat/articulos_textos/mle_poisson_demostracion/MLE.html},
langid = {es}
}